Wydział Matematyki, Informatyki i Mechaniki UW
| Typ | Tytuł | Opis | Dziedzina | Termin |
|---|---|---|---|---|
| Spotkanie festiwalowe | O grach, dzięki którym dowiadujemy się czegoś o sobie |
Zgoda buduje, a niezgoda rujnuje... zupełnie dosłownie. Przeanalizujemy kilka prostych gier, w których gracze przekonują się, że próba wyśrubowania indywidualnego zysku prowadzi do strat całej społeczności i każdego z osobna. Okaże się, że wprowadzenie podatku może paradoksalnie wzbogacić podatników, zamknięcie drogi - zredukować korki, a wprowadzenie możliwości karania łamiących zasady społeczne - doprowadzić do spirali przemocy. Całość jest na tyle prosta, że pozwala brać udział już gimnazjalistom - starsi docenią natomiast klarowność matematycznego opisu za pomocą pojęć teorii gier. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Grafy losowe - od kombinatoryki do modelowania sieci społecznych |
Grafy są jednym z najprostszych obiektów matematycznych - poznajemy je już w szkole podstawowej. Niemniej lista ich zastosowań obejmuje wiele zagadnień, od informatyki poprzez nauki fizyczne i biologiczne do nauk społecznych, gdzie używane są m. in. do opisu sieci relacji międzyludzkich. Grafy, które pojawiają się w tych zastosowaniach, mogą zmieniać się w czasie, a ich struktura często zależy od czynników losowych. Właściwy opis losowości ma zatem istotne znaczenie dla zrozumienia zjawisk opisywanych przez graf. Podczas wykładu omówię podstawowe modele grafów losowych i ich zastosowania, koncentrując się na wpływie losowego mechanizmu tworzenia grafu na jego strukturę. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Zadania z ekstremalnością w tle |
Zaprezentuję rozwiązania kilku kombinatoryczno-geometrycznych problemów, w których ważną rolę odgrywa pojęcie ekstremalności. Skoncentruję się na przykładach, w których ekstremalizowane obiekty nie pojawiają się explicite w sformułowaniu problemu, ale których wprowadzenie staje się narzędziem pozwalającym uchwycić i wykorzystać istotne elementy struktury problemu i w łatwy sposób prowadzą do jego rozwiązania. Osoby przyzwyczajone do algorytmicznych zadań znanych z licealnych lekcji matematyki będą mogły spojrzeć na królową nauk z nieco innej perspektywy. Matematyka nie jest przecież bynajmniej powielaniem schematów. Każdy z rozważanych podczas wykładu problemów żyje swym własnym życiem, ekstremalność jest tutaj jedynie ogólną metodą wymagającą czasem nie lada pomysłowości przy jej stosowaniu. Jednocześnie rozwiązania w ten sposób uzyskane są eleganckie, nietrudne do zrozumienia i mogą być z powodzeniem przyswojone przez zdolnych uczniów szkoły podstawowej. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Interpretacje kombinatoryczne, czyli o tym, jak użyć królików doświadczalnych w matematyce |
W wykładzie przedstawię technikę rozwiązywania równań przez interpretacje kombinatoryczne. Technika ta polega na opowiedzeniu prostej historii, która opisuje (interpretuje) skomplikowane wyrażenie matematyczne. Opowiedzenie tej samej historii inaczej pozwala często na przedstawienie tego samego wyrażenia w inny, prostszy sposób. Za elementarny przykład może nam posłużyć pokazanie, że współczynnik dwumianowy
|
Nauki matematyczne |
|
| Spotkanie festiwalowe | Przygody Bajtazara, czyli zaproszenie do Olimpiady Informatycznej |
W tym roku Olimpiada Informatyczna skończyła 25 lat. Olimpiada to zawody indywidualne przeznaczone dla uczniów szkół średnich, choć mogą w niej brać udział uczniowie gimnazjów i szkół podstawowych. Łącznie w pierwszych etapach Olimpiady wystartowało 21 989 uczniów. Uczestnicy Olimpiady muszą wykazać się umiejętnościami analizowania problemów obliczeniowych, układania wydajnych algorytmów i implementowania ich w językach programowania wysokiego poziomu, doboru stosownych struktur danych, testowania programów i pracy w środowisku programistycznym - po prostu muszą działać tak, jak zawodowi informatycy. Najlepsi uczestnicy Olimpiady reprezentują Polskę na Międzynarodowej Olimpiadzie Informatycznej i w innych zawodach międzynarodowych, osiągając znaczące sukcesy. Ukoronowaniem tych sukcesów było dwukrotne zwycięstwo indywidualne Polaka w Międzynarodowej Olimpiadzie Informatycznej, w 2006 i 2007 roku. To, co wyróżnia Olimpiadę Informatyczną, to ambitne i inspirujące zadania. Rozwiązanie zadania olimpijskiego jest źródłem satysfakcji, a trudności napotkane przy próbie rozwiązania stymulują do poszukiwań, dyskusji i samokształcenia. Wiele zadań na Olimpiadzie Informatycznej dotyczy problemów, które powstają w wyimaginowanym królestwie Bajtocji, a główną postacią jest w nich mieszkaniec tej krainy, Bajtazar. "Przygody Bajtazara" to także tytuł okolicznościowej książki zawierającej wybór 50 zadań z wszystkich edycji Olimpiady Informatycznej, która została wydana w tym roku z okazji 25-lecia Olimpiady. Podczas prezentacji przedstawię, w sposób zrozumiały dla niespecjalisty, przykłady zadań olimpijskich oraz przedstawię najważniejsze osiągnięcia Olimpiady i jej uczestników. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Kilka naprawdę ładnych zadań, czyli zaproszenie do Olimpiady Matematycznej |
Wykład dedykowany jest uczniom, którzy nie mieli wcześniej styczności z Olimpiadą Matematyczną. Opowiemy na nim, jak wyglądają kolejne etapy olimpiady i przedstawimy kilka zadań ze wcześniejszych edycji zawodów. Kilka ostatnich minut poświęcimy pytaniom słuchaczy. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Bitcoin i inni - kryptografia a kryptowaluty |
Podczas wykładu można będzie bliżej poznać kryptowaluty. Zacznę od bitcoina i kryjącej się za nim matematyki, a następnie przejdę do Ethereum i "inteligentnych kontraktów". Na zakończenie opowiem o problemach i ograniczeniach dzisiejszego świata kryptowalut. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Kolorowa matematyka |
Stoisko "Kolorowa matematyka" prezentuje w formie zagadek logicznych, kolorowanek i zabaw ruchowych całkiem poważne zagadnienia matematyczne: 1) Twierdzenie o czterech barwach, które mówi, że każdą mapę można tak pokolorować czterema barwami, że sąsiednie państwa są różnych kolorów. 2) Wstęgę Mobiusa, czyli kartkę papieru, która ma tylko jedną stronę (i kilka innych zdumiewających cech). 3) Problem komiwojażera, czyli zaskakująco trudne zadanie znalezienia najkrótszej drogi odwiedzającej zadane punkty na mapie. 4) Wieże Hanoi, czyli układankę, w której chodzi o to, żeby ją ułożyć, robiąc jak najmniej ruchów. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Sprytne strategie o podłożu kombinatorycznym |
Omówione zostanie pojęcie permutacji zbioru skończonego, a następnie podstawowe obserwacje związane z jej rozkładem na cykle. Część zajęć będzie dotyczyć opisu kombinatorycznego, część zaś - zjawisk związanych z losowością. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Grafy, cykle, łamigłówki |
Grafy stanowią pożyteczne narzędzie do modelowania rozmaitych problemów, od projektowania sieci komunikacyjnych i układów elektronicznych, przez wyszukiwanie tras w nawigacji samochodowej, do zastosowań w chemii, biologii, socjologii i sztucznej inteligencji. Na wykładzie skoncentruję się jednak raczej na bardziej rozrywkowych zastosowaniach: Które figury dają się narysować bez odrywania ołówka od papieru? Jak przyspieszyć odgadywanie zapomnianego PINu do cyfrowego zamka? Jak rozwiązać problem Wież z Hanoi bez użycia rekursji? Na wykładzie opowiem o tych i innych zastosowaniach cykli Eulera i Hamiltona w grafach w szeroko rozumianej matematyce rekreacyjnej. |
Nauki matematyczne |
|
| Spotkanie festiwalowe | Wyjaśnienie pewnej zagadki w ekologii |
Historia modelu Lotki-Volterry i wyjaśnienie tajemnicy, jak I wojna światowa wpłynęła na zwiększenie procentu dużych drapieżnych ryb w Adriatyku. Model Lotki-Volterry jest przykładem prostego układu równań, który wyjaśnia zjawiska niewyjaśnialne bez matematyki. |
Nauki matematyczne |
|


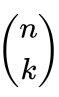 jest równy współczynnikowi
jest równy współczynnikowi 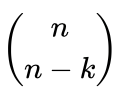 . Ten pierwszy możemy zinterpretować następująco: Załóżmy, że mamy w hodowli n królików. Współczynnik
. Ten pierwszy możemy zinterpretować następująco: Załóżmy, że mamy w hodowli n królików. Współczynnik